Exercices : Théorème de Thalès 3e
Classe:
Troisième
Exercice 1
Calculer dans les cas suivants :
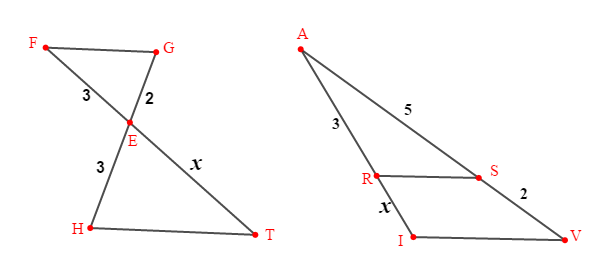
Exercice 2
Dans les cas suivants, les droites et sont- elles parallèles ?
cas :
cas :
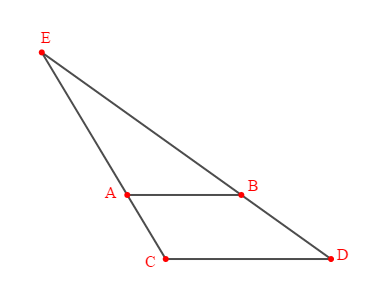
Exercice 3
est un trapèze de bases et ; et
La parallèle à passant par coupe en et en
1) Faire la figure.
2) Quelle est la nature du quadrilatère ? En déduire puis
3) Soit un point de tel que . Montrer que les droites et sont parallèles.
Exercice 4
On considère le triangle rectangle en tel que et
1) Calculer
2) Le cercle de centre et de rayon 6 coupe en
Soit un point du segment tel que
Démontrer que puis calculer
Exercice 5
est un rectangle : . est un point de tel que . et se coupent en
1) Calculer et .
2) est un point de tel que et un point de tel que , démontre que
Exercice 6
On considère deux cercles et tangents extérieurement en . est une droite tangente à et à respectivement en et
La droite coupe en
1) Démontrer que .
2) a) On pose ; exprime en fonction de puis calcule
b) En déduire la valeur exacte de .
c) Démontre que .
3) Soit le point de tel que . Démontrer que
Exercice 7
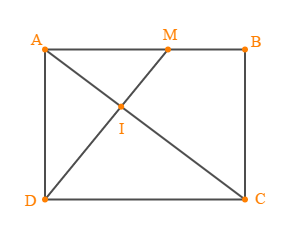
est un carré. le point de tel que . est le point de tel que
1) Démontrer que les droites et sont parallèles.
2) a) Par quel nombre doit-on multiplier la longueur pour obtenir la longueur ? Justifie la réponse donnée.
b) Par quel nombre doit-on multiplier l'aire du triangle pour obtenir l'aire de ? Justifier.
Exercice 8
On donne trois points du plan et alignés dans cet ordre sur une droite tels que et
est un réel positif.
Sur une droite passant par et distincte de .
On prend deux points et tels que et un point sur tel que
1) Faire la figure ; puis démontrer que
2) Calculer en fonction de .
Exercice 9
Construire un triangle tel que
1) Le triangle est-il rectangle ? Justifier.
2) Marque un point sur tel que puis tracer la droite passant par et parallèle à la droite , elle coupe en Calculer et
3) On donne et Déterminer la valeur de puis la valeur de
Exercice 10
Soit un triangle tel que et . est le point du coté tel que
1) La parallèle à passant par coupe le coté en . Calculer
2) La perpendiculaire à passant par coupe en et en . Calculer
3) Soit un point de la parallèle à passant par , on appelle respectivement et les intersections de et avec la droite . Calculer puis
Exercice 11
est un triangle est un point de la droite
La droite passant par et parallèle à la droite coupe la droite au point
La droite passant par et parallèle à la droite coupe la droite au point
Démontrer que
Exercice 12
est un triangle tel que et
Soit le point de tel que :
La parallèle à passant par coupe en
Calculer et
Exercice 13
Dans le plan, on considère un triangle rectangle en tel que : et
1) Faire une figure complète puis calculer
2) On considère le point , tel que : soit un point du segment et
3) a) Soit le point de la droite dont la projection orthogonale sur est le point
b) Montrer que les droites et sont .
c) Calculer les distances et
4) Calculer l'aire de et le coefficient de réduction des longueurs. En déduire l'aire de
Exercice 14
Soit un triangle tel que : et
1) Montrer que est un triangle rectangle en
2) Soit le point du segment tel que
La perpendiculaire à passant par coupe au point
a) Montrer que et sont parallèles.
b) Calculer les distances et
Exercice 15
1) Soit un cercle de centre et de rayon un de ses diamètres.
a) D'un côté de la droite , construire le point tel que le triangle soit équilatéral.
b) De l'autre côté de la droite , placer le point du cercle , tel que
2) Démontrer que le triangle est équilatéral.
3) On admet que les angles et sont égaux. En déduire la position relative de et
4) La droite coupe le segment en et en En utilisant le théorème de Thalès justifier que :
Exercice 16
Construire un rectangle tel que : et On désigne par un point tel que
Par , on trace la parallèle à qui coupe en et la parallèle à qui coupe en
1) Calculer puis exprimer et en fonction de
2) Montrer que est indépendant de
3) Pour quelles valeurs de à t-on
Exercice 17
1) Énonce dans ton cahier le théorème de Thalès.
2) Énonce dans ton cahier la réciproque du théorème de Thalès.
Exercice 18
Donne la ou les figures présentant deux triangles en position de Thalès.
...................................................................................................
...................................................................................................
...................................................................................................
...................................................................................................
...................................................................................................
....................................................................................................
Exercice 19
Réponds par vrai ou faux :
1) est un triangle, et tels que :
, d'après la réciproque du théorème de Thalès
2) Si est un triangle ; , , d'une part et , , d'autre part sont alignés dans le même ordre et
alors
3) Si deux triangles sont en position de Thalès alors les supports de deux de leurs côtés sont parallèles.
4) et sont deux triangles tels que alors et sont en position de Thalès.
5) Si est un triangle, et la parallèle à passant par coupe en alors et sont des triangles en position de Thalès.
Exercice 20
est un trapèze rectangle tel que , et
1) Fais la figure en vraie grandeur que tu compléteras au fur et à mesure.
2) Calcule et
3) La perpendiculaire à la droite passant par coupe en
Montre que
4) Soit le point de la droite n'appartenant pas à tel que
Démontre que et sont parallèles.
5) Calcule
Exercice 21
et sont deux droites sécantes en
et ,
et ;
et ,
et
a) Fais la figure.
b) Calcule
c) et tel que :
,
Les droites et sont elles parallèles ?
Exercice 22
1) Construis un triangle tel que , et
2) Place sur le segment le point tel que et sur le segment le point tel que
3) Démontre que les droites et sont parallèles.
4) Place le point sur le segment tel que
La parallèle à la droite passant par coupe la droite en
Calcule et
Exercice 23
Sur la figure ci-dessous,
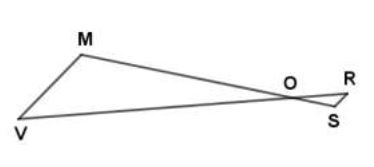
, , et ,
1) Montre que les droites et sont parallèles.
2) Calcule
Exercice 24
Soient , et trois points alignés dans cet ordre sur une droite tels que et
et sont deux cercles de diamètres respectifs et
Place un point sur le cercle tel que
1) Donne en justifiant, la nature du triangle
2) Calcule la longueur
3) La droite coupe le en
a) Donne en justifiant, la nature du triangle puis démontre que
b) Calcule les longueurs et
Exercice 25
1) Soit un cercle de centre et de rayon et un de ses diamètres.
a) Dans l'un des demi-plans de frontière , construis le point tel que le triangle soit équilatéral.
b) Dans l'autre demi-plan, place le point du cercle tel que
2) Démontre que le triangle est équilatéral.
3) Justifie que les angles et sont égaux puis déduis-en la position relative des droites et
4) La droite coupe en et en
En utilisant le théorème de Thalès, justifie que
Exercice 26
1) Construis un triangle rectangle en tel que :
et
2) Calcule
3) Place le point tel que , puis trace la parallèle à passant par qui coupe en
4) Calcule les distances et
5) Soit l'aire du triangle et celle du triangle
Montre que
6) Construis sur , le point tel que puis sur le point tel que et
7) Démontre que les droites et sont parallèles.
Exercice 27
Dans le plan, on considère un triangle rectangle en tel que :
et
1) Fais une figure complète puis calcule
2) Place le point , tel que soit un point de et
3) Soit le point de la droite dont la projection orthogonale sur est le point
a) Montre que les droites et sont parallèles.
b) Calcule les distances et
Exercice 28
La figure ci-dessous donne le schéma d'une table à repasser.
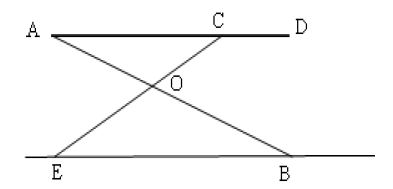
Le segment représente la planche.
Les segments et représentent les pieds.
Les droites et se coupent en
On donne :
;
;
;
;
;
1) Montre que la droite est parallèle à
2) Calcule l'écartement en
3) Le triangle est-il rectangle ?
Justifie ta réponse.
Exercice 29
1) Construis le triangle tel que :
;
;
2) Construis le point de tel que :
3) La parallèle à passant par coupe en
a) Démontre que
b) Calcule
4) Calcule
5) La parallèle à passant par coupe en
La parallèle à passant par coupe en
Démontre que :
Exercice 30
Soit le triangle tel que :
, et
est le point du côté tel que
1) La parallèle à passant par coupe le côté en
Calcule la longueur
2) La perpendiculaire à passant par coupe en et en
Calcule
3) Soit un point de la parallèle à passant par , on appelle respectivement et les intersections de et avec la droite
a) Calcule
b) Calcule